数位DP

数位DP是什么？

数位是指把一个数字按照个、十、百、千等等一位一位地拆开，关注它每一位上的数字。如果拆的是十进制数，那么每一位数字都是 0~9，其他进制可类比十进制。

数位 DP：用来解决一类特定问题，这种问题比较好辨认，一般具有这几个特征：

1. 要求统计满足一定条件的数的数量（即，最终目的为计数）；

2. 这些条件经过转化后可以使用「数位」的思想去理解和判断；

3. 输入会提供一个数字区间（有时也只提供上界）来作为统计的限制；

4. 上界很大（比如 10^{18}），暴力枚举验证会超时。

数位 DP 的基本原理：

考虑人类计数的方式，最朴素的计数就是从小到大开始依次加一。但我们发现对于位数比较多的数，这样的过程中有许多重复的部分。例如，从 7000 数到 7999、从 8000 数到 8999、和从 9000 数到 9999 的过程非常相似，它们都是后三位从 000 变到 999，不一样的地方只有千位这一位，所以我们可以把这些过程归并起来，将这些过程中产生的计数答案也都存在一个通用的数组里。此数组根据题目具体要求设置状态，用递推或 DP 的方式进行状态转移。
数位 DP 中通常会利用常规计数问题技巧，比如把一个区间内的答案拆成两部分相减，比如求某个区间[x-y]中满足某个条件的数的个数，可以使用dp[y]-dp[x]来得出答案
那么有了通用答案数组，接下来就是统计答案。统计答案可以选择记忆化搜索，也可以选择循环迭代递推。为了不重不漏地统计所有不超过上限的答案，要从高到低枚举每一位，再考虑每一位都可以填哪些数字，最后利用通用答案数组统计答案。

• 以上内容摘自OI-WIKI中关于数位DP的介绍

数位DP的普遍做法

数位DP通常要求将区间最大值N拆为B进制的各个位(以10进制为例)， 假设N在10进制下有n位，则N可以用下式表示：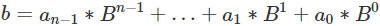

从最高位开始，由于所在区间挑选的所有数不能大于N，则对于每个位来说，可选的数为0-a[i]-1 和 a[i]两种情况(根据特定题目，可选的数还会进一步缩小)， 若当前位选择0-a[i]-1，则之后的各个位可以随心所欲的挑选符合题意的数，若当前位选择a[i]，则后一位也必须分成两种情况来讨论，DP的过程可以用二叉树来进行模拟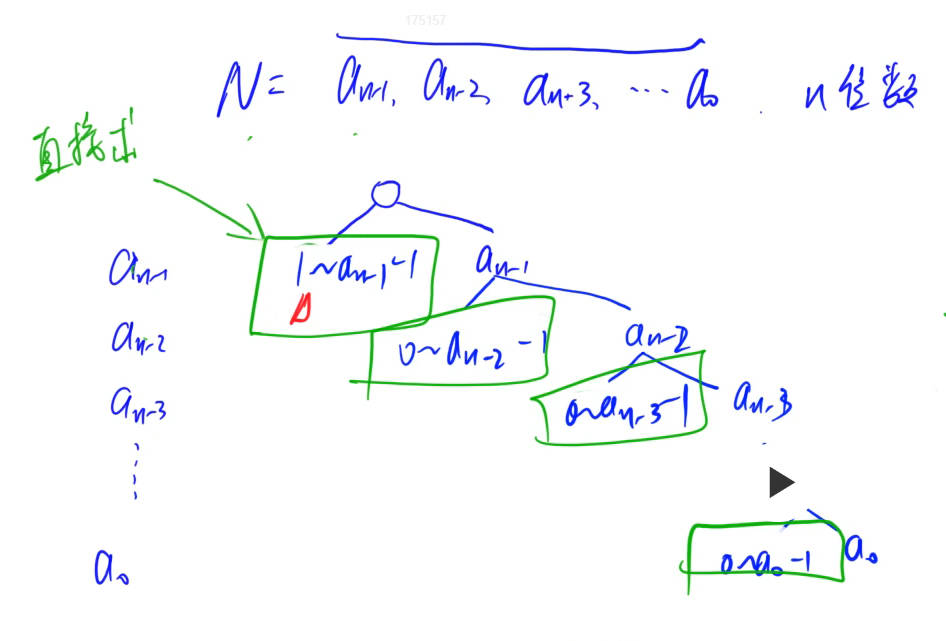

左边的分支即为挑选比当前位小的数，最右边的分支表示选择的数即为原数，左边分支由于后续不再受到N的限制，可以直接用组合数或者动态规划的方式求得所有情况，于是不必要继续分支下去，最右边的分支表示1种情况，并且最后需判断原数是否满足题意即可

介绍一道例题，来自力扣：902.最大为N的数字组合
根据评论区star靠前的各个题解，我总结出了三种解法：

1. 最接近所述数位DP原理和普遍做法的题解

对 x 进行「从高到低」的处理（假定 x 数位为 nnn），对于第 k 位而言（k 不为最高位），假设在 x 中第 k 位为 cur，那么为了满足「大小限制」关系，我们只能在 [1,cur−1] 范围内取数，同时为了满足「数字只能取自 nums」的限制，因此我们可以利用 nums 本身有序，对其进行二分，找到满足 nums[mid] <= cur 的最大下标 r，根据 nums[r] 与 cur 的关系进行分情况讨论：

• nums[r] = cur: 此时位置 k 共有 r 种选择，而后面的每个位置由于 nums[i] 可以使用多次，每个位置都有 m 种选择，共有 n-p 个位置，因此该分支往后共有 r*m的n-p次方 种合法方案。且由于 nums[r] = cur，往后还有分支可决策（需要统计），因此需要继续处理；
• nums[r]<cur：此时算上 nums[r]，位置 k 共有 r+1 种选择，而后面的每个位置由于 nums[i] 可以使用多次，每个位置都有 m 种选择，共有 n−p 个位置，因此该分支共有 **(r+1)m的n-p次方* 种合法方案，由于 nums[r]<cur，往后的方案数（均满足小于关系）已经在这次被统计完成，累加后进行 break；
• nums[r]>cur：该分支往后不再满足「大小限制」要求，合法方案数为 0，直接 break。
  其他细节：实际上，我们可以将 res1 和 res2 两种情况进行合并处理。

宫水三叶,数位DP+二分

该实现的时间复杂度为O(log10 N)代码如下：

class Solution {
public:
    std::vector<int> nums;
    int dp(int x) {
        std::vector<int> list;
        while (x != 0) {
            list.push_back(x % 10);
            x /= 10;
        }
        int n = list.size(), m = nums.size(), ans = 0;
        //p指的是目前遍历了几个位
        for (int i = n - 1, p = 1; i >= 0; i--, p++) {
            int cur = list[i];
            int l = 0, r = m - 1;

            while (l < r) {
                int mid = (l + r + 1) / 2;
                if (nums[mid] <= cur)
                    l = mid;
                else
                    r = mid - 1;
            }

            if (nums[r] > cur) {
                break;
            } else if (nums[r] == cur) {
                ans += r * static_cast<int>(std::pow(m, n - p));
                if (i == 0)
                    ans++;
            } else if (nums[r] < cur) {
                ans += (r + 1) * static_cast<int>(std::pow(m, n - p));
                break;
            }
        }
        // 位数比x小的话，从1位数到n-1位数，每个位都可填m个数
        for (int i = 1, last = 1; i < n; i++) {
            int cur = last * m;
            ans += cur;
            last = cur;
        }
        return ans;
    }

    int atMostNGivenDigitSet(std::vector<std::string>& digits, int max) {
        int n = digits.size();
        nums.resize(n);

        for (int i = 0; i < n; i++)
            nums[i] = std::stoi(digits[i]);

        return dp(max);
    }
};

2. 动态规划

先看代码:

class Solution {
public:
    int atMostNGivenDigitSet(vector<string>& digits, int n) {
        string s = to_string(n);
        int m = digits.size(), k = s.size();
        /*dp数组表示前i位由digits中的数字构造并且前i位所表示的数字小于n的所有数数量*/
        vector<int> dp(k + 1, 0);
        /*last 表示前i-1是否为n的前i-1位，即是否为最大值， nlast表示当前位是否会出现n的第i位
        若出现且last为真，则进入最右分支，否则进入左子分支*/
        int last = 1, nlast = 0;
        for (int i = 1; i <= k; i++) {
            for (int j = 0; j < m; j++) {
                if (digits[j][0] == s[i-1]) {
                    nlast = last;
                    // dp[i]++;
                } else if (digits[j][0] < s[i-1]) {
                    /*若last为假，则不需要考虑当前位要小于n的当前位的状况，之后会将其一并加入*/
                    dp[i] += last;
                } else {
                    break;
                }
            }
            if (i > 1) {
                /**/
                dp[i] += m + dp[i - 1] * m;
            }
            /*更新last并重置nlast*/
            last = nlast;
            nlast = 0;
        }
        return dp[k] + last; 
    }
};

状态转移方程为：
dp[i]=m+dp[i−1]×m+last×C[i]
迭代过程中用last来记录是否还受到N的约束，m 就是 dp[i] 中单个字符所组成的数量，相当于 res3， C[i] 表示nums中小于N当前第i位的个数，这里其实相当于将第一种解法所述的 res1 和 res2 动态的在迭代过程中求出，dp[i-1] * m表示早就进入了左边的分支，但是并没有一并求出，last * C[i] 表示在此次迭代才进入了最右分支的左边分支， 最后的加last就是将最右边分支的一种情况加上

3. 递归 + 记忆化搜索(最难理解的一个解法)
   先看代码:

int atMostNGivenDigitSet(vector<string>& digits, int n) {
        auto s = to_string(n);
        int m = s.length(), dp[m];
        memset(dp, -1, sizeof(dp));
         function<int(int, bool, bool)> f = [&](int i, bool is_limit, bool is_num) -> int {
             if (i == m) return is_num;
             if(!is_limit && is_num && dp[i] >= 0) return dp[i];
             int res = 0;
             if (!is_num) res = f( i + 1, false, false);
             char up = is_limit ? s[i] : '9';
             for(auto& d : digits) {
                 if( d[0] > up) break;
                 res += f(i + 1, is_limit && d[0] == up, true);
             }
             if(!is_limit && is_num)dp[i] = res;
             return res;
         };
         return f(0, true, false); 
    }

将 n 转换成字符串 s，定义 f(i,isLimit,isNum) 表示构造从左往右第 i 位及其之后数位的合法方案数，其中：

isLimit表示当前是否受到了 n 的约束。若为真，则第 i 位填入的数字至多为 s[i]，否则至多为 9。
isNum 表示 i 前面的数位是否填了数字。若为假，则当前位可以跳过（不填数字），或者要填入的数字至少为 1；若为真，则必须填数字，且要填入的数字从 0 开始。这样我们可以控制构造出的是一位数/两位数/三位数等等。对于本题而言，要填入的数字可直接从 digits 中选择。
枚举要填入的数字，具体实现逻辑见代码。

代码中 Java/C++/Go 只需要记忆化 i，因为：

对于一个固定的 i，它受到 isLimit 或 isNum 的约束在整个递归过程中至多会出现一次，没必要记忆化。
另外，如果只记忆化 iii，dp 数组的含义就变成在不受到 n 的约束时的合法方案数，所以要在 !isLimit && isNum 成立时才去记忆化。

灵神数位 DP 通用模板 + 详细注释 + 题单（Python/Java/C++/Go）